Working Classes

What is a class? If you dabble in computational design or BIM management long enough you will no doubt end up digging through RhinoCommon, RevitAPI, or some other API reference document. I recall my first forays into these inscrutable and endless lists of familiar-looking yet also somewhat-alien entries. Almost everything is listed as being a "class"—so what is that?

Chapter 6 of Code Complete is titled "Working Classes" and covers the fundamental concepts and best practices for implementing these work horses of object-oriented programming. Simply put, a class is a collection of data and routines that share a cohesive and well-defined purpose. That "cohesive and well-defined" part is super important, because classes that adhere to the Single Responsibility Principle (which states: "A class should have only one reason to change"¹) allow us to greatly minimize the amount of complexity (and code) we humans need to consider at any given moment. The last chapter was all about aggressively limiting complexity, and well-designed classes are one of the most effective tools for accomplishing that.

Another very helpful way of considering classes is to view them through the lens of abstract data types (ADTs). Every introductory coding course will start by teaching you the basics of data types (integers, booleans, characters, etc.). An abstract data type is a programming entity that simplifies an object that could otherwise be very complicated to define. Let's take a simple example and consider point objects in Rhino. A point, otherwise known as Point3d in RhinoCommon, is a spatial thing you can interact with in the Rhino viewport. We can use points to define more complex things like lines and surfaces. We can also use more fundamental things (numbers, to be exact) to define the points themselves. Everyone familiar with the idea of Cartesian space knows that a point has an x, y, and z value. When we interact with points as an abstract data type, we can disregard those three xyz coordinates because we know the point object encompasses its own place in space.

The concept of an ADT is so helpful because it allows us to perform operations on things that are meaningful to us and relevant to the problem domain. A line is easy to conceptualize as being formed by two points—a line defined by six numbers not so much. At a glance, which of the following snippets of code make more sense to you?

// Constructing a line from two ADTs
var line1 = new Line(PointA, PointB);

// Constructing a line from six primitives
var line2 = new Line(0.734, 9.454, 1.492, 2.409, 4.501, 3.008);

In RhinoCommon, both are completely acceptable ways of making a line, but the first one is much easier for humans to grasp. Using ADTs results in code that is more obviously correct (or more obviously wrong, if that's the case). The code is also self-documenting; it states what it is in terms that apply to the real world, and we typically find it a lot easier to work with real world entities. To give a graphic example of how ADTs fit into the scheme of classes, consider this simple Grasshopper script:

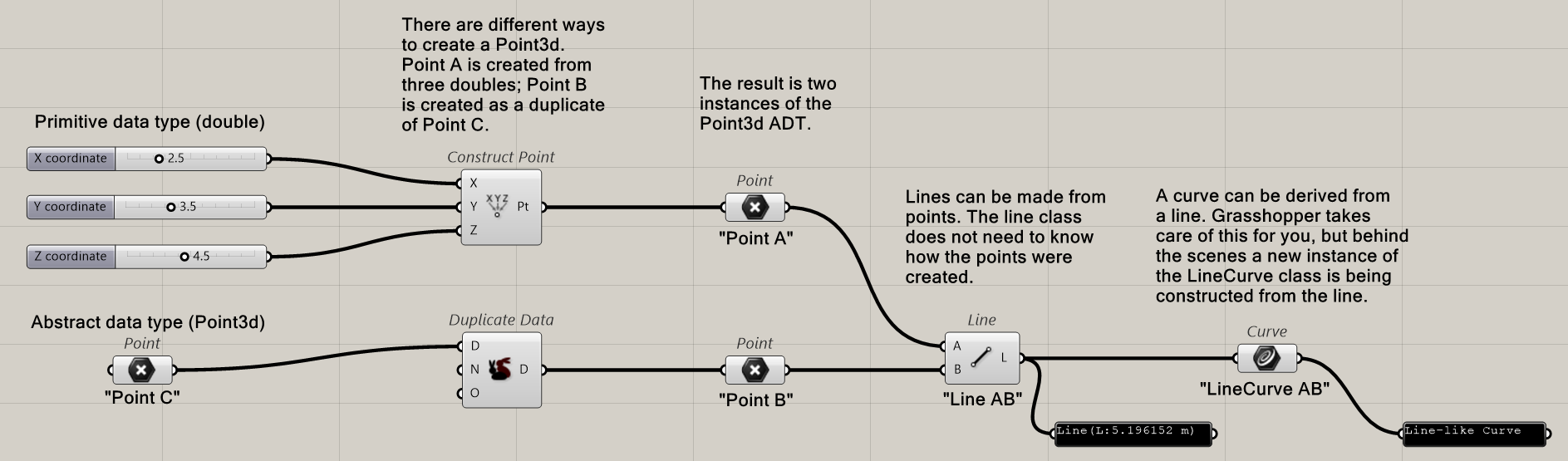
This script shows two points being created and used to create a line, which is itself used to create a line-like curve in Rhino. At the beginning of the script, we see three numbers and a point; this is the raw material to be used in the creation of our points. At the next stage, we see two different methods for creating new Point3d objects; the first uses primitive data types and the second uses an existing Point3d ADT. In terms of classes, these are what we call constructors, and a class can have many different ones. Once the Point3d constructors are called, we end up with two instances of that class (PointA and PointB). These instances are then fed into the Line class to produce a line. Further on, we see an instance of the LineCurve class being created from a Line input. Each of these classes has constructors that make use of ADTs: Point3d can be made from another point; Line can be made from two points; and LineCurve can be derived from a line.

Point3d pointA = new Point3d(2.5, 3.5, 4.5);
Point3d pointB = new Point3d(pointC);

Line lineAB = new Line(pointA, pointB);

LineCurve lineCurveAB = new LineCurve(lineAB);

Points and curves make for rather simple examples of abstraction; we only cut out a few parameters from our scope of attention. Imagine, however, trying to keep track of all the parameters that make up all the things that make up a curtain wall system; fortunately there is a class in Revit that abstracts this very complex assembly into a single ADT:

Understanding the concept of abstract data types is important to building useful classes, but to adequately explain classes we need to add a couple of additional concepts: inheritance and polymorphism. Understanding these two words in the context of programming is key to understanding how software like Rhino and Revit handle geometric data. As you might imagine, inheritance describes a condition by which one entity can inherit certain qualities from an ancestor. In this case, the ancestor is a more abstract class that is semantically related to the class in question. To explain this, it's quite common to use examples like Car and Truck (which inherit from Vehicle), or Cat and Dog (which inherit from Animal). Since this is a blog about programming for designers, I'll stick with geometry. If you were paying close attention to the short Grasshopper script above, you might have noticed that when we connected the "Line" component to a "Curve" parameter, we did not, in fact, end up with a "Curve." What we got instead was a "Line-like curve." What's the deal with that?

In this case, Grasshopper detects that the curve input is a Line object and automatically invokes the appropriate LineCurve constructor. This is a great example of why using Grasshopper is such an intuitive way for people to learn computational thinking, but it also demonstrates why it can be difficult for people to switch from visual programming to a text-based coding. In this case, it's not apparent why we get a line-like curve when we really wanted a regular old curve. Well, in a sense we did get get what we wanted, as there are many sub-classes that all inherit from the curve class. What does that mean? It means that line curves (and arc curves, and polyline curves) all share certain qualities that allow us to deal with them on a more abstract level. These specific types of curves all inherit certain qualities of "curveness" from the parent class, and in some cases we can treat them all as if they were the same thing. Regard the Grasshopper script below:

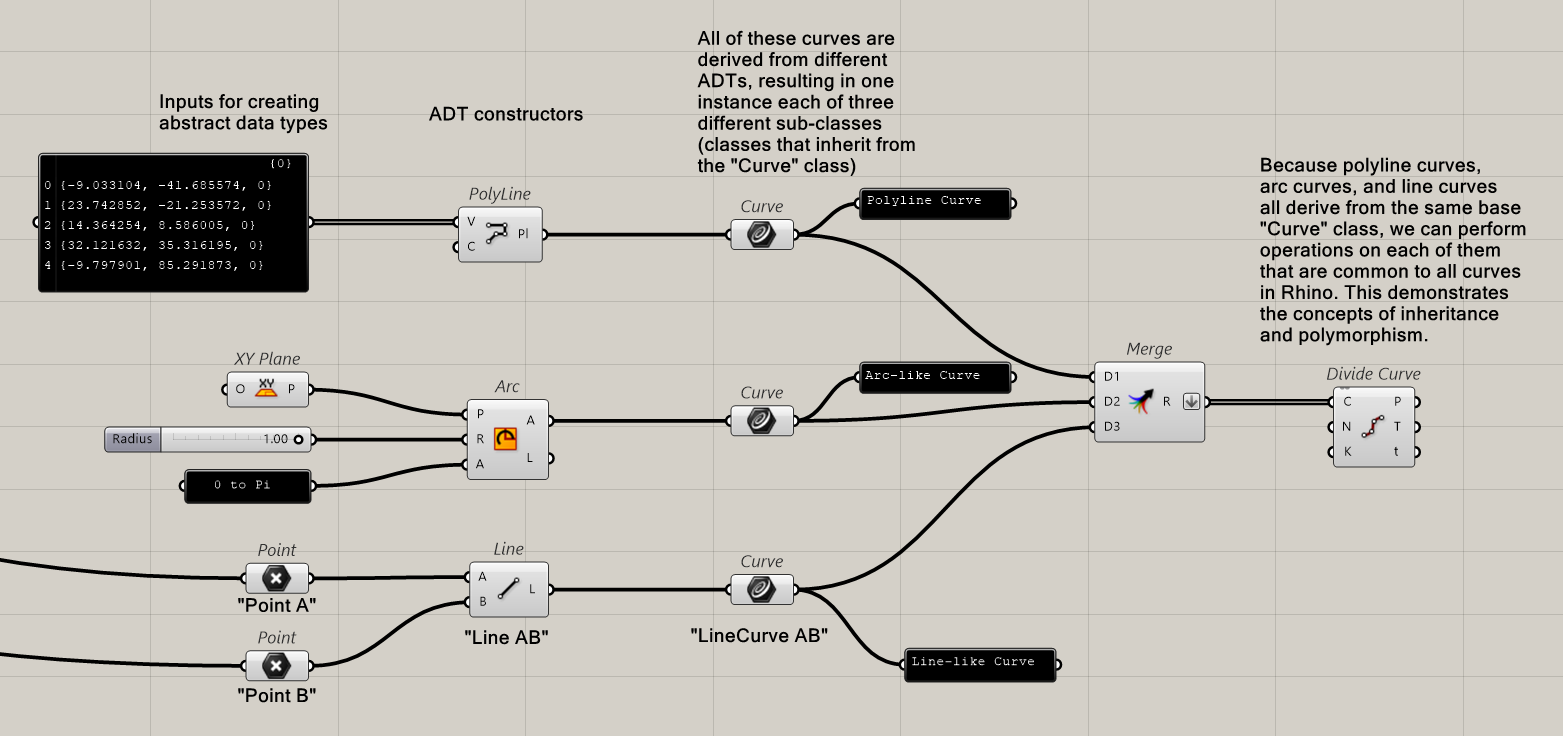
The left hand side of the script shows the process of building up a few ADTs from different kinds of inputs, which we have already covered. From a polyline, an arc, and a line, we get instances of three different sub-classes that inherit from the Curve class. They each have certain properties that are unique to their geometry—an ArcCurve has a radius, a PolylineCurve has a certain number of points, and a LineCurve has a mathematically defined line inherent to it. These three curves also contain a number of properties that they all share: they all have a start and end point, with a certain tangent vector at each; they all are either closed or not; they all have a certain domain and degree. In other words, they all inherit these properties from the parent Curve class.

Inheritance, when employed with care and consideration, is a powerful tool for reducing complexity in a program. Just imagine how much more code you would have to write to allow for each of these kinds of curves to access all these properties and methods without inheritance:

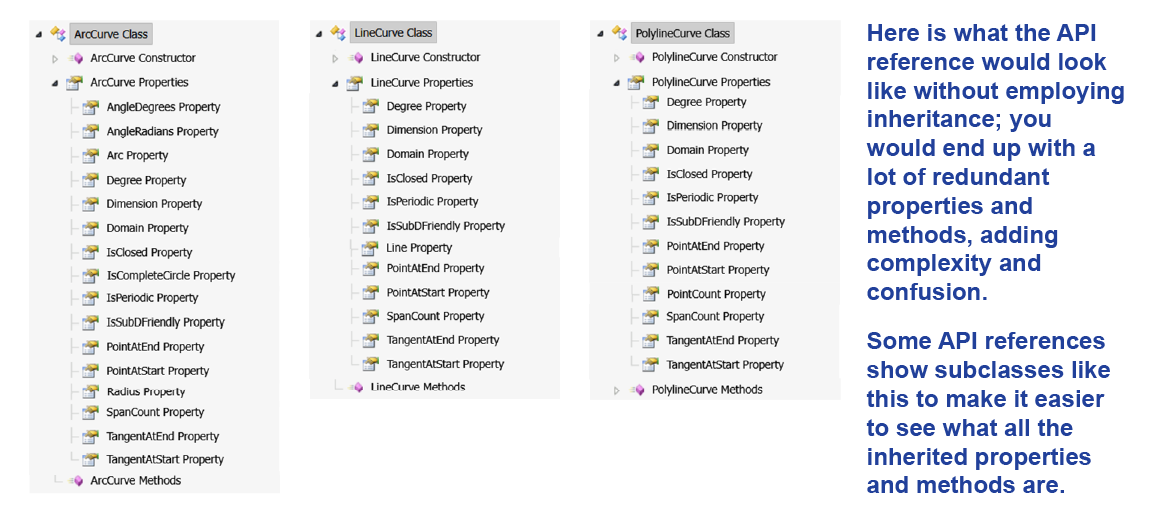
We can, in fact, perform all of the Curve methods on all of these different kinds of curves without regard for exactly what sort of curve they are. To the right side of the script above, we see the three different types of curve all being fed into the "Divide" component. Curve.DivideByCount will operate just fine on any object that inherits from Curve. This is polymorphism—the ability for semantically related subtypes to be substituted for one another with respect to their inherited qualities. Closely related to this concept is the Liskov Substitution Principle, which is another important rule for building robust and rigorous code. I won't dive in too deeply, but in essence the LSP demands that you enforce strong semantic interoperability between base class and sub-class—i.e. respect polymorphism absolutely with no exceptions.

Savvy readers will have noticed that I'm leaving out one important concept for class definition in object-oriented programming: interfaces. Since I'm trying to keep my post length under 1,500 words (which I've already failed to do today), I've decided to simplify things to some extent. For those who don't already know what I'm referring to, I will simply say that interfaces are another kind of thing that classes can inherit from. An interface is like a class, except it doesn't tell you how to accomplish anything—just that you need to accomplish it. Essentially, it's a contract rather than a blueprint. In C#, classes can inherit from a base class and an interface at the same time. Consider this example:

public class Dog : Animal, IMammalian

Our Dog object is, indeed, an animal, but not all animals are mammals. In this case, the IMammalian interface acts as a contract that obligates the Dog class to address certain requirements—for example, that there should be a Dog.NurseOffspring() method available. The interface does not indicate how the class should implement nursing offspring, as mammals nurse their young in many different ways. We then know that any object that inherits from IMammalian will be able to nurse offspring, even if we don't know how they do it. This is a gross simplification of the topic, but I think it's sufficient for understanding what classes are for and how they work.

Altogether, by employing the concepts of abstract data types, inheritance, and polymorphism, we are able to create working classes that help limit complexity while also affording us powerful efficiencies in programming. Well-designed classes allow us to hierarchically build up complexity. Every time we climb to a higher level we can disregard the implementation details of everything that got us there. The examples used in this post all come from existing codebases; we can't access the implementation details of these Revit and Rhino classes, but we can draw lessons from their organization and structure when thinking about how to build our own. In Chapter 6 of Code Complete, Steve McConnell offers lots of advice for when and how to create your own classes, but in the interest of brevity (or at least in the interest of refraining from long-windedness), I'll leave it to curious readers to investigate more closely. The next chapter is titled "High-Quality Routines," so we should be able to delve more deeply into the nuts and bolts of class code-writing.

References

¹ Martin, Robert C. (2003). Agile Software Development, Principles, Patterns, and Practices. Prentice Hall. p. 95. ISBN 978-0135974445.